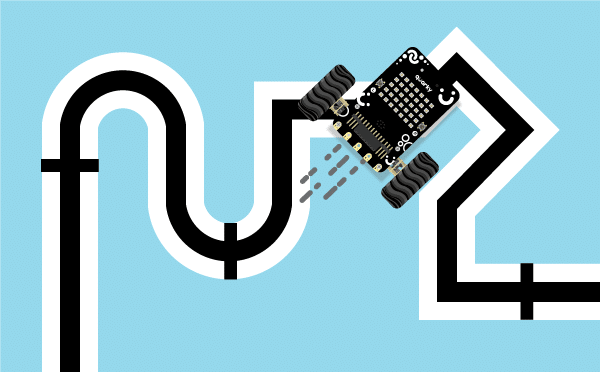
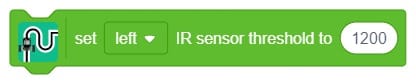
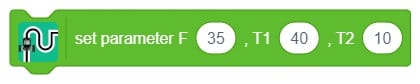
Proportional, Integral, and Derivative (PID) functions are used to improve the feedback (analog inputs from the IR Sensors) to improve the robot’s movement.

1. Proportional (P) :
This component enables the robot to make immediate, precise adjustments based on its distance from the line. If the robot drifts too far to the right, it will steer left, and if it veers too far to the left, it will steer right to correct its course.
2. Integral (I) :
The integral component monitors how long the robot has been off the line. If the deviation persists for an extended time, this part applies a larger correction to bring the robot back on track more effectively.
3. Derivative (D) :
The derivative component anticipates future errors by analyzing the rate at which the robot drifts from the line. This ensures smooth, predictive adjustments, helping to prevent overshooting and maintain stability.
The control output is given by:
Control Output = Proportional + Integral + Derivative
So, the PID controller combines these three components to continuously adjust the robot’s movements, keeping it as close to the line as possible while moving smoothly and fast. A robot is always learning and fine-tuning its path to stay on track.
Think of it as a smart system that balances and corrects itself as it moves, ensuring it follows the line accurately. PID line followers are commonly used in robotics competitions and educational settings to teach about control systems and automation.
Note: If you initialize a Three IR line following, use Kp (propositional constant) >= 7 for a better result.
How does PID work in the Quarky Line Following?
In Quarky’s “Do Line Following” Block/Python function, the system employs its two Infrared (IR) sensors, one on the left and another on the right, to navigate along a line.
Let’s say the analog values registered by these sensors
on a white surface are
Left = 150
Right = 170
while on the black line, they read
Left = 820
Right = 750.
When the robot is shifted to the right, the left sensor is on the black line and the right one is on the white. At this point the reading of IR Sensors is
Left = 820
Right = 170,
The error is calculated as follows:
Error = (Left Sensor Value – Right Sensor Value)/10
= (820 – 170)/10
= 65
Proportional Only
For the PID (Proportional-Integral-Derivative) controller, the constants are set as follows:
Kp = 0.5, Ki = 0, and Kd = 0.
The proportional term is then calculated.
Proportional = K_p *Error
= 0.5* 65
= 32 (approximately)
The control output is given by:
Control Output = Proportional + Integral + Derivative
In this case, both the integral and derivative terms are set to 0, so the control output simplifies to:
Control Output = 32 + 0 + 0
= 32
Subsequently, the motor speeds are adjusted based on the control output and the motor speed parameters.
Assuming base speed = 40, minimum speed = 0, and maximum speed = 80
The Left and Right motor speeds are computed as follows:
Left Motor Speed = Base Speed – Control Output
= 40 – 32
= 8
Right Motor Speed = Base Speed + Control Output
= 40 + 32
= 72
Proportional and Integral only
The integral term in the PID (Proportional-Integral-Derivative) controller addresses the accumulated past errors over time. If there has been a persistent error over time, the integral term gradually increases, helping to eliminate the accumulated error.
In a scenario where the robot is stuck and the robot’s tires are slipping due to the excessive weight of the robot and low battery, both sensors are placed on contrasting surfaces – the Left sensor on black and the Right sensor on white. Despite the challenging conditions, the proportional constant (Kp) comes into play, initially adjusting the motor speeds. As a result, the Left motor speed becomes 8, and the Right motor speed reaches 72.
When an integral term with a constant value (Ki = 0.01) is introduced into the control equation, the integral value is updated in each iteration:
I = I + error
I = 0 + 65 = 65
The control output, comprising proportional, integral, and derivative terms, is then computed as follows:
Control Output = Proportional +Integral + Derivative
= (0.5 * 65) + (0.01 * 65) + 0
= 32.65
Left Motor Speed = 7.35
Right Motor Speed = 72.65
In the subsequent loop, the integral term is updated again:
I = I + error
I = 65 + 65 = 130
And the control output in the next iteration becomes:
Control Output = (0.5 * 65) + (0.01 * 130) + 0
= 33.3
Left Motor Speed = 6.7
Right Motor Speed = 73.3
Proportional, Integral, and Derivative
Derivative (D): The derivative term in the PID (Proportional-Integral-Derivative) controller anticipates future errors by assessing how fast the error is changing. It plays a crucial role in preventing overshooting or oscillations by slowing down the control action as the system approaches the setpoint.
In a small arena, when a robot needs to execute a significant turn or a U-turn, increasing the proportional constant (Kp) may result in excessive oscillations. To address this, the derivative term is introduced to control oscillations and overshooting.
Consider a scenario where the error is increased:
Error = (Left Sensor Value – Right Sensor Value)/10
=(930 – 170)/10
= 76
The derivative term is computed as:
D = Previous Error – Error
= 65 – 76
= -11
The control output, including proportional, integral, and derivative terms, is then calculated as follows:
Kp = 0.5, Ki = 0.01, and Kd = 0.2
Control Output = Proportional + Integral + Derivative
= (0.5 * 76) + (0.01 * 76) + (0.2 * -11)
= 38 + 0.76 – 2.2 = 36.56
Subsequently, the left and right motor speeds are adjusted:
Left Motor Speed = 3.44
Right Motor Speed = 76.56
In the subsequent loop, the integral term is updated, and the process repeats with a new error:
Error = (600 – 170)/10
= 43
The integral term is updated:
I = I + Error
= 76 + 43
= 109
The derivative term for the new error is computed:
D = Previous Error – Error
= 76 – 43
= 33
The control output remains the same in this loop:
Control Output = (0.5 * 43) + (0.01 * 109) + (0.2 * 33)
= 21.5 + 1.09 + 6.6
=29.19
Left Motor Speed = 10.81
Right Motor Speed = 69.19
This iterative process continues, with the derivative term helping to manage the robot’s response to changing errors, ultimately enhancing its stability.